MCMC(Markov Chain Monte-Carlo)를 통해 생성한 데이터를 활용하기 위해서는 마르코프 체인(Markov Chain)이 정상상태(Stationary)에 수렴(Convergence)해야 한다. 이를 확인하고 다루는 방법에 대해 다룰 것이다.
1. Trace plot
2. 자기상관성(Autocorrelation)
3. 초기 단계(Burn-in period)
1. Trace plot
MCMC의 수렴을 확인하는 가장 직관적인 방법은 데이터의 생성 과정을 직접 그림으로 나타내는 것이다. 시행횟수에 따른 생성된 데이터의 분포를 통해 이를 확인할 수 있다.
In:
log_g <- function(mu, n, ybar) {
mu2 <- mu^2
return(n * (ybar * mu - mu2 / 2.0) - log(1.0 + mu2))
}
mh_sampl <- function(n_data, ybar, n_iter, mu_init, prop_sd) {
mu_out <- numeric(n_iter)
accpt_cnt <- 0
mu_now <- mu_init
log_g_now <- log_g(mu_now, n_data, ybar)
for (i in 1:n_iter) {
mu_cand <- rnorm(1, mu_now, prop_sd)
log_cand <- log_g(mu_cand, n_data, ybar)
log_alpha <- log_cand - log_g_now
alpha <- exp(log_alpha)
if (runif(1) < alpha) {
mu_now <- mu_cand
accpt_cnt <- accpt_cnt + 1
log_g_now <- log_cand
}
mu_out[i] <- mu_now
}
return(list(mu = mu_out, accpt_rate = accpt_cnt/n_iter))
}
y = c(-0.2, -1.5, -5.3, 0.3, -0.8, -2.2)
ybar = mean(y)
n = length(y)
library(coda)
post_sampl_1 = mh_sampl(n_data = n, ybar = ybar, n_iter = 1e3, mu_init = 0.0, prop_sd = 1.0)
traceplot(as.mcmc(post_sampl_1$mu))
post_sampl_2 = mh_sampl(n_data = n, ybar = ybar, n_iter = 1e3, mu_init = 0.0, prop_sd = 0.05)
traceplot(as.mcmc(post_sampl_2$mu))
post_sampl_3 = mh_sampl(n_data = n, ybar = ybar, n_iter = 1e4, mu_init = 0.0, prop_sd = 0.05)
traceplot(as.mcmc(post_sampl$mu_3))
Out:
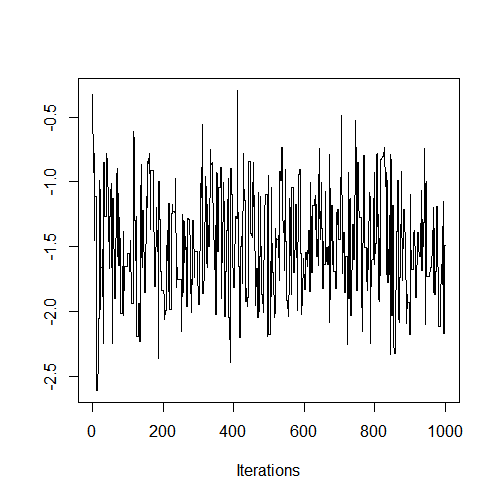

▷ 위의 그림은 MCMC의 일반적인 방법인 Metropolis-Hastings(이하 MH) 알고리즘을 적용하여 나타난 결과이다. 이 포스팅의 모든 그림과 분석은 MH 알고리즘의 결과로부터 구하였다.
▷ 첫 번째 그림를 보다시피 생성된 데이터가 정규분포 형태를 띄며 수렴하고 있는 것을 확인할 수 있다. 이처럼 추세(Trend)가 보이지 않고, 평균이 일정한 상태를 나타내고 있으면 마르코프 체인이 수렴한다고 볼 수 있다.
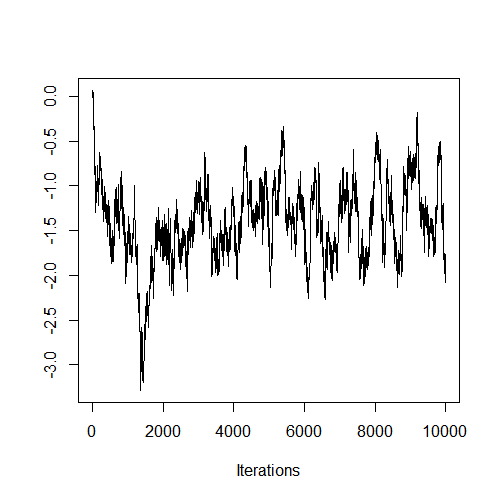
▷ 두 번째 그림은 시행횟수가 증가할 수록 감소하는 경향을 보이고 있으며, 평균이 일정하지 않다. 따라서 마르코프 체인이 수렴한다고 볼 수 없다.
▷ 세 번째 그림은 두 번째 그림의 데이터 생성 조건(제안분포의 평균, 표준편차)과 같게 한 뒤, 더 많은 데이터를 생성한 결과이다. 초기 시행에서는 감소하는 경향이 나타나지만, 2000번 시행 이후부터 추세가 보이지 않고, 평균이 일정한 것을 확인할 수 있다. 이는 제안 분포의 표준편차가 낮아서 마르코프 체인의 수렴속도가 느려졌기 때문에 나타난 결과이다. 즉, MH 알고리즘을 통한 마르코프 체인의 수렴속도는 제안 분포의 표준편차에 따라 결정된다.
2. 자기상관성
자기상관성은 데이터의 현재 시점과 과거 시점을 비교하여 얼마나 선형 의존(Linearly dependent)인지를 나타내는 지표로 -1과 1사이의 값으로 나타난다. 아래의 그림를 통해 자기상관성을 확인해보자.
In:
traceplot(as.mcmc(post_sampl_1$mu))
autocorr.plot(as.mcmc(post_sampl_1$mu))
traceplot(as.mcmc(post_sampl_2$mu))
autocorr.plot(as.mcmc(post_sampl_2$mu))
Out:

▷ 첫 번째 줄의 그림은 시차(Lag)가 20인 지점에서 자기상관성이 거의 나타나지 않지만, 두 번째 줄의 그림에서는 시차가 30인 지점까지 자기상관성이 높게 나오는 것을 확인할 수 있다. MCMC로부터 생성된 데이터의 자기상관성은 그 데이터가 가진 정보량으로 해석할 수 있다. 따라서 자기상관성이 낮은 첫 번째 줄의 생성된 데이터가 두 번째 줄의 경우보다 더 많은 정보를 가지고 있다고 볼 수 있다.
▶ 데이터에 자기상관성이 나타나지 않는다는 것은 각 데이터가 이전 시점의 데이터에 영향을 받지 않는 의미이다. MCMC의 특성상 각 시점의 정보를 이용하여 다음 시점의 데이터를 생성하기 때문에 자기상관관계가 나타날 수 밖에 없다. 따라서 생성된 데이터의 ESS(Effective Sample Size)를 구하기 위해서는 자기상관성을 제거해야한다.
▶ ESS는 MCMC를 통해 생성된 데이터 중 독립인 데이터의 갯수를 의미한다.
데이터의 자기상관성을 제거하고 목적 분포(Target distribution)에 대한 ESS(Effective Sample Size)를 구하여보자.
In:
post_sampl_4 = mh_sampl(n_data = n, ybar = ybar, n_iter = 1e6, mu_init = 0.0, prop_sd = 0.05)
traceplot(as.mcmc(post_sampl_4$mu))
autocorr.plot(as.mcmc(post_sampl_4$mu), lag.max = 2500)
thin_intverval = 300
thin_idx = seq(from = thin_intverval,
to = length(as.mcmc(post_sampl_4$mu)),
by = thin_intverval)
traceplot(as.mcmc(post_sampl_4$mu[thin_idx]))
autocorr.plot(as.mcmc(post_sampl_4$mu[thin_idx]), lag.max = 750)
Out:

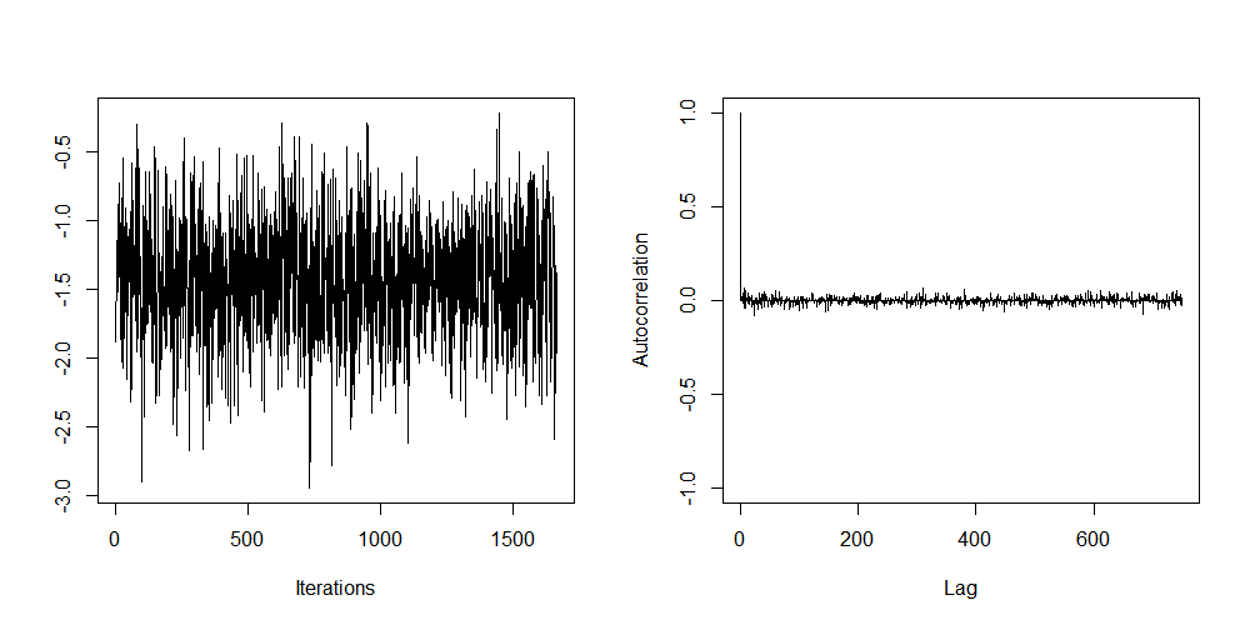
▷ 첫 번째 줄의 그림을 통해 마르코프 체인이 수렴하는 것과 시행횟수가 300인 지점부터 자기상관성이 줄어들어 거의 나타나지 않는 것을 확인할 수 있다.
▷ 두 번째 줄의 그림은 첫 번째 줄의 생성된 데이터로부터 시행횟수가 300단위인 지점의 데이터를 뽑아내어 생성과정과 자기상관성에 대해 그림을 그린 것이다. 첫 번째 줄의 그림과는 다르게 자기상관성이 나타나지 않는 것을 확인할 수 있다. 즉, 각 데이터가 이전 시점의 데이터와 독립적임을 알 수 있다.
In:
length(thin_idx)
effectiveSize(post_sampl_4$mu)
Out:
[1] 3333
var1
3366.361
▷ 추출한 데이터의 갯수와 ESS를 구하는 함수인 effectiveSize()의 결과가 다 3,300대로 비슷한 것을 확인할 수 있다.
In:
raftery.diag(post_sampl_4$mu)
Out:
Quantile (q) = 0.025
Accuracy (r) = +/- 0.005
Probability (s) = 0.95
Burn-in Total Lower bound Dependence
(M) (N) (Nmin) factor (I)
390 435500 3746 116
▶ raftery.diag()는 추정하고자 하는 추정치에 필요한 데이터의 갯수에 대해 Raftery and Lewis's diagnostic을 통해 알려주는 함수이다.
▶ 마르코프 체인이 수렴하기까지 필요한 시행횟수는 Burn-in, 추정에 필요한 최소의 데이터 갯수는 Total, 추정에 필요한 자기상관성이 0인 데이터의 갯수는 Lower bound로 나타낸다. Dependence factor는 Burn-in과 Total의 합을 Lower bound로 나눈 것으로 얼마나 데이터의 자기상관성이 높은지를 의미한다.
▷ raftery.diag()를 이용한 결과, 위의 추정치를 추정하기 위해 생성해야하는 최소 데이터의 수는 435,500개인 것으로 나타났고, 자기상관성이 0인 데이터의 수 최소 3,746개가 필요한 것으로 나타났다.
3. 초기 단계
trace plot을 이용하여 마르코프 체인의 수렴을 확인하는 방법을 알아보았다. 하지만, 이는 정성적인 방법이기에 주관적일 수 있다. 따라서 정량적인 방법이 요구되는데, Gelman-Rubin diagostic을 이용하여 정량적으로 확인할 수 있다.
Gelman-Rubin diagostic을 이용하여 마르코프 체인의 수렴을 확인하여보자.
In:
post_sampl_1 = mh_sampl(n_data = n, ybar = ybar, n_iter = 1e3, mu_init = 50, prop_sd = 0.5)
post_sampl_2 = mh_sampl(n_data = n, ybar = ybar, n_iter = 1e3, mu_init = 25, prop_sd = 1.0)
post_sampl_3 = mh_sampl(n_data = n, ybar = ybar, n_iter = 1e3, mu_init = -25, prop_sd = 0.5)
post_sampl_4 = mh_sampl(n_data = n, ybar = ybar, n_iter = 1e3, mu_init = -50, prop_sd = 1.0)
idx = 1:length(post_sampl_1$mu)
list_post = mcmc.list(as.mcmc(post_sampl_1$mu), as.mcmc(post_sampl_2$mu),
as.mcmc(post_sampl_3$mu), as.mcmc(post_sampl_4$mu))
traceplot(list_post)
gelman.diag(list_post)
Out:

Potential scale reduction factors:
Point est. Upper C.I.
[1,] 1.01 1.03
▷ Gelman-Rubin diagostic을 통해 수렴을 확인하기 위해서는 서로 다른 초기값을 가진 마르코프 체인을 만들어주어야 한다. 이는 Gelman-Rubin diagostic은 초기값이 서로 다른 마르코프 체인의 변동성(Variability)를 비교하여 구하기 때문이다. 따라서 초기값이 다른 4개의 마르코프 체인을 만들었고, 위의 그림에서 수렴 과정을 확인할 수 있다.
▷ Gelman-Rubin diagostic은 1에 가까울 수록 모든 마르코피 체인이 수렴한다는 것을 의미한다. 따라서 Galman-Rubin diagostic의 점 추정치가 1.01이고 신뢰상한이 1.03이므로, 4개의 마르코프 체인은 수렴한다고 할 수 있다.
In:
gelman.plot(list_post)
Out:

▷ gelmen.plat()을 통해 시행횟수가 500인 지점부터 1에 가까워짐을 확인할 수 있다. 즉, 시행횟수가 500인 지점의 데이터를 버리고, 나머지 데이터를 목적함수로부터 생성된 데이터로 활용하면 된다.
Reference:
"Bayesian Statistics: From Concept to Data AnalysisTechniques and Models," Coursera, https://www.coursera.org/learn/bayesian-statistics/.
'Statistics > Bayesian Statistics' 카테고리의 다른 글
| DIC(Deviance Information Criterion) (0) | 2020.08.18 |
|---|---|
| 베이지안 선형 회귀(Bayesian linear regression) (0) | 2020.08.17 |
| 깁스 샘플링(Gibbs sampling) (0) | 2020.08.14 |
| JAGS(Just Another Gibbs Sampler) 사용법 (0) | 2020.08.11 |
| 메트로폴리스 헤이스팅스 알고리즘(Metropolis-Hastings algorithm) (1) | 2020.08.11 |



