깁스 샘플링(Gibbs sampling)

🌻Pep🌻 2020. 8. 14. 06:08

깁스 샘플링(Gibbs sampling)에 대해 알아볼 것이다. 다룰 내용은 다음과 같다.

1. 깁스 샘플링

2. 깁스 샘플링의 예제

1. 깁스 샘플링

깁스 샘플링은 Metropolis Hastings(이하 MH) 알고리즘의 특별한 형태로, 제안 분포(Proposal distribution)를 자신의 Full conditional distribution로 두어 샘플링하는 방법이다. 이렇게 함으로써, 각 시행에서 발생하는 데이터에 대해 Acceptance probability는 1이 되는 성질을 가지게 된다. 다음의 증명을 통하여 이를 확인해보자.

▷ 제안 분포를 Full conditional posterior로 둠으로써 미세 균형 조건(Detailed balance condition)이 성립하게 된다. 따라서 alpha를 통해 전이확률(Transition probability)을 보정할 필요 없이, 매 시행에서 생성한 데이터를 받아들이면(Accept) 된다.

깁스 샘플링의 알고리즘은 다음과 같다.

▷ 위의 알고리즘은 모수가 2개인 경우에 대한 것이고, 이를 일반화하면 여러 개의 모수의 사후분포로부터 데이터 생성을 할 수 있다.

2. 깁스 샘플링의 예제

문제)

아래 모델의 모수인 mu와 sigma^2를 사후분포로부터 데이터를 생성하시오.

풀이)

▷ Full joint posterior을 정리하면 위의 식을 구할 수 있다. 이때, 각 모수에 대하여 full conditional posterior을 구하려면 Full joint posterior에서 관심 모수를 제외한 다른 모수는 상수로 취하고, 이를 통해 분포를 추론한다. mu와 sigma^2는 모두 켤레사전분포로써 사전분포와 사후분포가 같은 분포를 따르는 것을 확인할 수 있다.

각 모수의 사후분포로부터 데이터를 생성하기 위해 깁스 샘플링 알고리즘을 적용하여 보자.

In:

update_mu = function(n, ybar, sig2, mu_0, sig2_0) {
  sig2_1 = 1.0 / (n / sig2 + 1.0 / sig2_0)
  mu_1 = sig2_1 * (n * ybar / sig2 + mu_0 / sig2_0)
  return(rnorm(n = 1, mean = mu_1, sd = sqrt(sig2_1)))
}

update_sig2 = function(n, y, mu, nu_0, beta_0) {
  nu_1 = nu_0 + n / 2.0
  sumsq = sum( (y - mu)^2 )
  beta_1 = beta_0 + sumsq / 2.0
  out_gamma = rgamma(n = 1, shape = nu_1, rate = beta_1)
  return(1.0 / out_gamma)
}

gibbs_sampl = function(y, n_iter, init, prior) {
  ybar = mean(y)
  n = length(y)
  
  mu_out = numeric(n_iter)
  sig2_out = numeric(n_iter)
  
  mu_now = init$mu
  
  for (i in 1:n_iter) {
    sig2_now = update_sig2(n = n, 
                           y = y, 
                           mu = mu_now, 
                           nu_0 = prior$nu_0, 
                           beta_0 = prior$beta_0)
    mu_now = update_mu(n = n, 
                       ybar = ybar, 
                       sig2 = sig2_now, 
                       mu_0 = prior$mu_0, 
                       sig2_0 = prior$sig2_0)
    
    sig2_out[i] = sig2_now
    mu_out[i] = mu_now
  }
  
  return(cbind(mu = mu_out, sig2 = sig2_out))
}

▷ update_mu()와 update_sigma()를 만들어 모수별 업데이트를 할 수 있도록 한다.

▷ gibs_sampl()은 깁스 샘플링 알고리즘에 따라 시행 횟수만큼의 데이터를 생성한다.

In:

y = c(1.2, 1.4, -0.5, 0.3, 0.9, 2.3, 1.0, 0.1, 1.3, 1.9)

ybar = mean(y)
n = length(y)

prior = list()
prior$mu_0 = 0.0
prior$sig2_0 = 1.0

prior$n_0 = 2.0
prior$s2_0 = 1.0
prior$nu_0 = prior$n_0 / 2.0
prior$beta_0 = prior$n_0 * prior$s2_0 / 2.0

init = list()
init$mu = 0.0

library('coda')

post_sampl = gibbs_sampl(y = y, n_iter = 1e3, init = init, prior = prior)

plot(as.mcmc(post_sampl))

summary(as.mcmc(post_sampl))

▷ y는 사후분포를 구하기 위한 데이터이다. prior에 사전분포의 모수에 대한 정보를 입력한다.

▷ init에 깁스 샘플링을 하기 위한 초기값을 주고, gibbs_sampl()을 통해 사후분포로부터 데이터를 생성한다.

▷ coda 패키지를 이용하여 plot()과 summary()를 통해 깁스 샘플링 과정과 결과에 대해 확인할 수 있다.

Out:

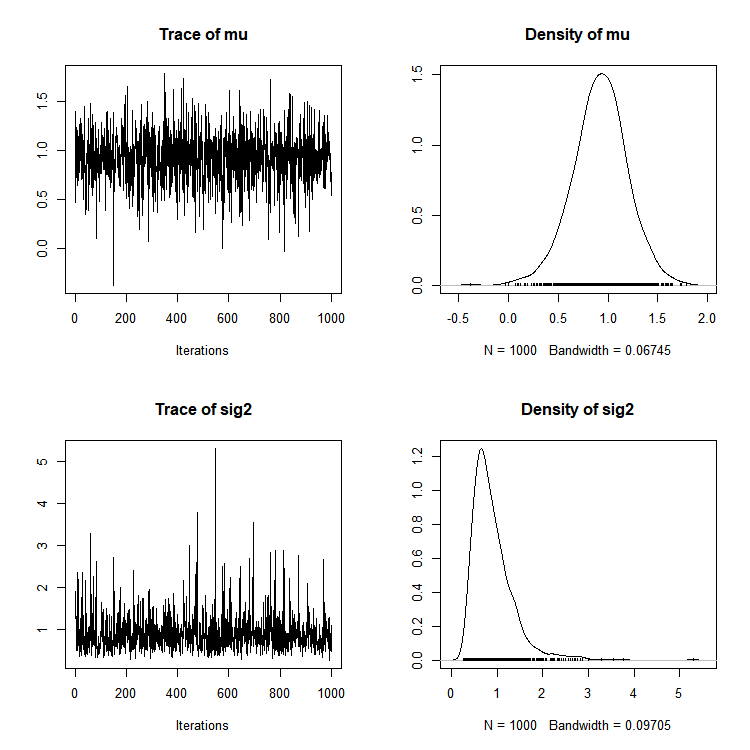
Iterations = 1:1000
Thinning interval = 1 
Number of chains = 1 
Sample size per chain = 1000 

1. Empirical mean and standard deviation for each variable,
   plus standard error of the mean:

       Mean     SD Naive SE Time-series SE
mu   0.9188 0.2758 0.008723       0.008723
sig2 0.9065 0.4727 0.014949       0.015826

2. Quantiles for each variable:

       2.5%    25%    50%   75% 97.5%
mu   0.3451 0.7533 0.9268 1.093 1.454
sig2 0.3796 0.5968 0.7957 1.085 2.179

Reference:

"Bayesian Statistics: From Concept to Data AnalysisTechniques and Models," Coursera, www.coursera.org/learn/bayesian-statistics/.

"(기계 학습, Machine Learning) Week 10 Sampling Based Inference | Lecture 7 Gibbs Sampling," AAILab Kaist, www.youtube.com/watch?v=Q9EYGw5QbHc&t=633s.